Imagine a network where information flows in one direction, like a river with no tributaries. That’s the essence of a directed acyclic graph (DAG). But how does this abstract concept translate into real-world applications?
What is a directed acyclic graph?
A directed acyclic graph (DAG) is a type of data structure where information flows in a specific direction, without any loops or cycles. It consists of nodes (vertices) connected by directed edges (arrows) that indicate the flow of information. The “acyclic” part means that there are no closed loops, so you cannot start at a node and follow a path back to the same node.
DAGs are used in various fields, including:
Blockchain Technology: Some newer blockchain projects use DAGs as an alternative to the traditional blockchain structure. In these systems, each transaction is a node in the DAG, and new transactions confirm previous ones, forming a web-like structure. This can offer potential advantages in scalability and transaction speed.
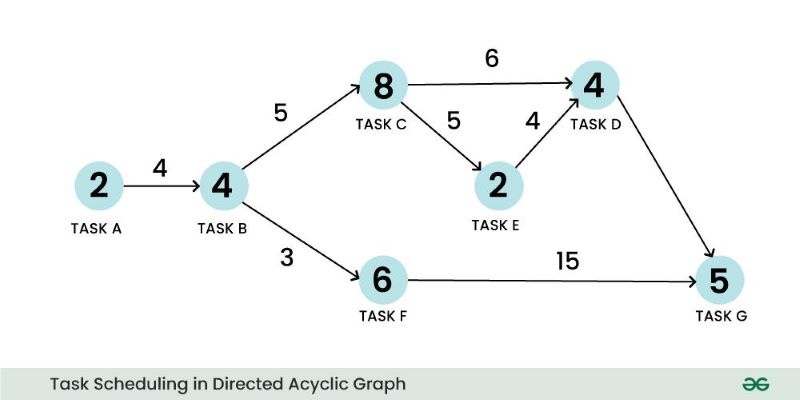
Task Scheduling: DAGs are used to model dependencies between tasks in project management and computing. This helps in optimizing task execution order and resource allocation.
Version Control Systems: DAGs represent the history of changes in version control systems like Git. Each commit is a node, and branches and merges create a DAG structure.
Data Processing Pipelines: DAGs model workflows in data processing and analysis, showing the sequence of operations and dependencies between them.
Meaning of directed acyclic graph
Directed acyclic graphs have two important characteristics:
Directed Edge s: In a Directed Acyclic Graph,each edge has a direction, meaning it goes from one vertex (node) to another. This direction represents a one-way relationship or dependency between nodes.
Cyclic: The term “ acyclic ” indicates that there are no cycles or closed loops in the graph. In other words, you cannot traverse a sequence of oriented edges and return to the same node, according to the direction of the edges. The formation of cycles is prohibited in DAG. So this feature is necessary.
Properties of directed acyclic graph DAG
Directed acyclic graphs (DAGs) have various properties that make them usable in graph problems.
There are the following properties of a Directed Acyclic Graph (DAG):
Reachability Relationship: In DAG, we can determine if there is a reachability relationship between two nodes. Node A is said to be reachable from node B if there exists a directed path starting at node B and ending at node A. This implies that you can follow the direction of edges in the graph to go from B to A.
Transitive Closure: A transitive closure of a directed graph is a new graph that represents all the direct and indirect relationships or connections between the nodes in the original graph. In other words, it tells you which nodes can be reached from other nodes by following one or more directed edges.
Transitive reduction: Transitive reduction of a directed graph is a new graph that retains only the essential, direct relationships between nodes, while eliminating any unnecessary indirect edges. In essence, it simplifies the graph by eliminating edges that can be inferred from the remaining edges.
Topological ordering: A DAG can be ordered topologically, which means you can linearly order its nodes in such a way that for all edges, the starting node of the edge appears first than in the chain. This property is useful for tasks such as planning and dependency resolution.
Practical applications of DAG
Directed Edge s: In a Directed Acyclic Graph,each edge has a direction, meaning it goes from one vertex (node) to another. This direction represents a one-way relationship or dependency between nodes.
Cyclic: The term “ acyclic ” indicates that there are no cycles or closed loops in the graph. In other words, you cannot traverse a sequence of oriented edges and return to the same node, according to the direction of the edges. The formation of cycles is prohibited in DAG. So this feature is necessary.
DAGs are powerful data structures with nodes connected by directed edges, creating a flow without cycles. They find applications in diverse fields, from blockchain technology to project management and compiler design. In blockchain, DAGs offer an alternative structure with potential scalability advantages. In project management, they model task dependencies for efficient scheduling. And in compilers, they analyze data flow for code optimization.
The versatility of DAGs makes them indispensable in various domains, offering efficient solutions for complex problems. Their unique properties and wide range of applications highlight their significance in modern computing and data management.
Dive deeper into the fascinating world of DAGs and their real-world impact. Subscribe to the Blockchain Bulletin Weekly newsletter for expert insights and in-depth analysis.